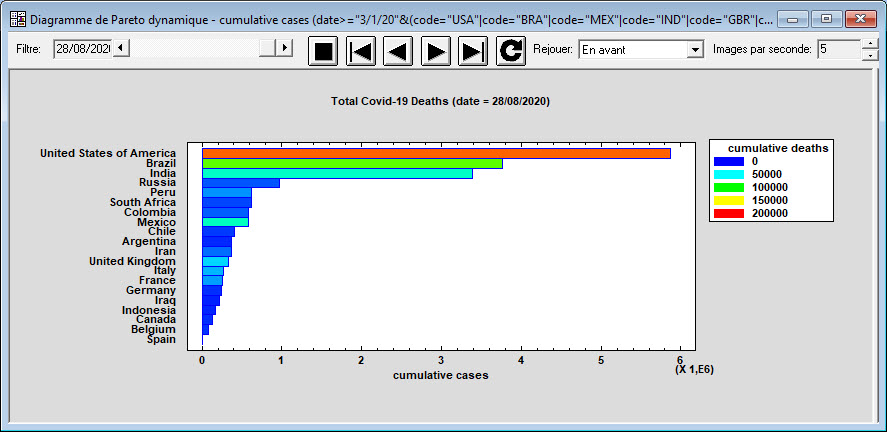
Diagramme de Pareto dynamique

La Statlet – Diagramme de Pareto dynamique est conçue pour afficher un diagramme de Pareto montrant comment les données d’un ensemble de catégories évoluent dans le temps. A partir de données représentant n catégories observées durant p périodes de temps, le logiciel crée un affichage dynamique illustrant comment chaque catégorie se modifie dans le temps.

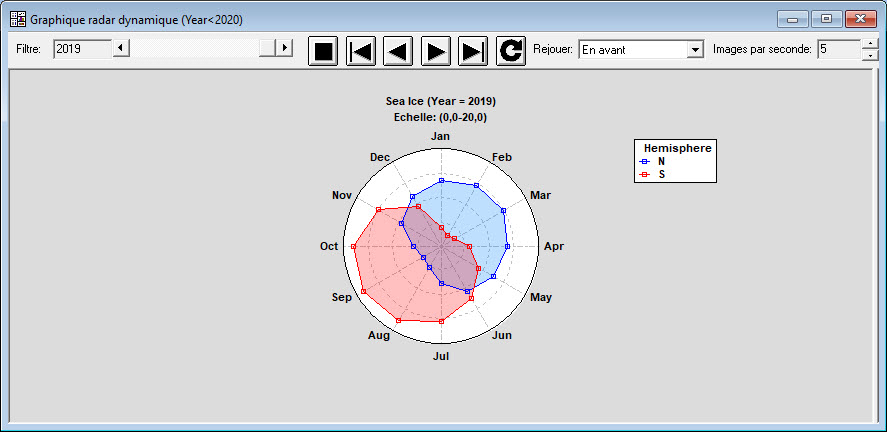
Graphique radar dynamique

La Statlet – Graphique radar dynamique est conçue pour montrer comment les données d’un ensemble de catégories ou de variables se modifient dans le temps. A partir de données constituées de k colonnes représentées sur p périodes de temps, le logiciel affiche un graphique dynamique que illustre comment chaque colonne se modifie. Des données classiques pour cette procédure sont, par exemple, des ventes mensuelles ou tout autre ensemble de données ayant de forts effets saisonniers.

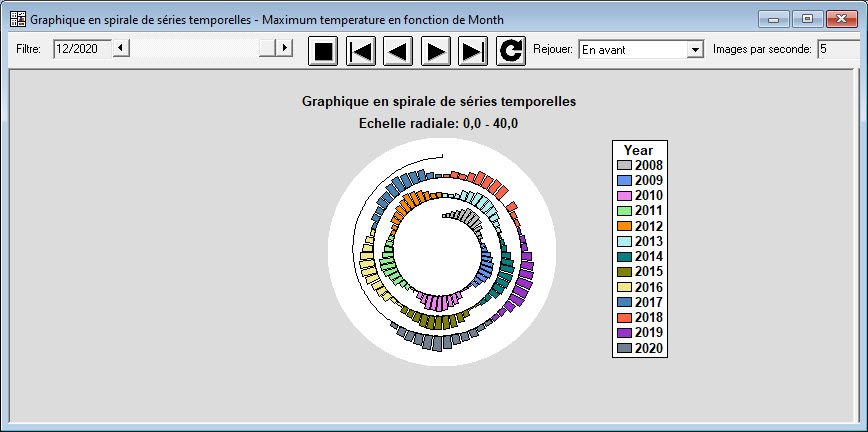
Graphique en spirale de séries temporelles

La Statlet – Graphique en spirale affiche des séries temporelles le long d’une spirale d’Archimède qui débute au centre du graphique et se déroule sous la forme d’une spirale. Cela est particulièrement utile pour afficher de grands volumes de données ayant une structure saisonnière. Les données peuvent être affichées sous la forme de bâtons, de points ou de lignes.

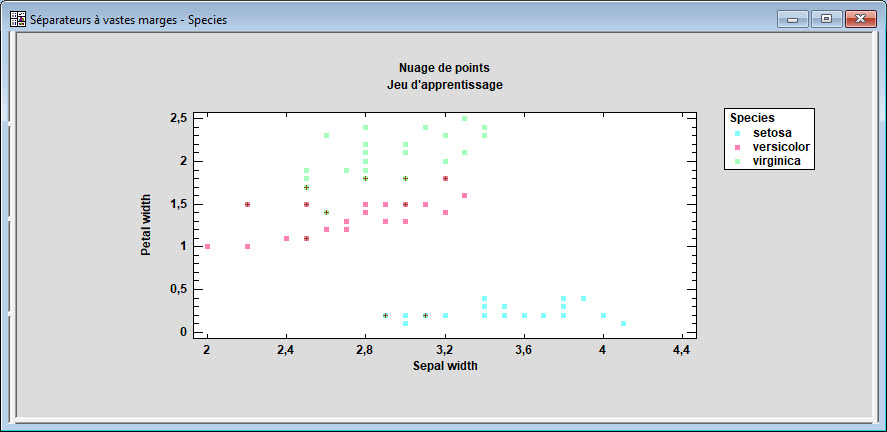
Séparateurs à vastes marges (SVM)

La procédure Séparateurs à Vastes Marges implémente une procédure d’apprentissage machine pour prévoir des observations à partir de données. Elle crée des modèles de deux formes : modèles de classement qui découpent des observations en groupes en se basant sur les caractéristiques observées, modèles de régression qui prévoient la valeur d’une variable à expliquer. Dans le cas d’un modèle de classement, l’algorithme découpent les observations en groupes en générant des marges autour des groupes aussi vastes que possible. Dans le cas d’un modèle de régression, l’algorithme minimise les coefficients d’un modèle dans lequel la distance des observations à une région autour du modèle ajusté définie par un montant d’erreur acceptable est aussi petite que possible. Les observations sont classiquement découpées en trois jeux : un jeu d’apprentissage utilisé pour construire le modèle, un jeu de validation pour lequel le groupe ou la valeur est connu, utilisé pour valider le modèle, un jeu de prévision pour lequel le groupe ou la valeur n’est pas connu, utilisé pour faire les prévisions désirées. La variable à expliquer peut être qualitative ou quantitative mais les facteurs prédictifs sont toutes quantitatifs. 

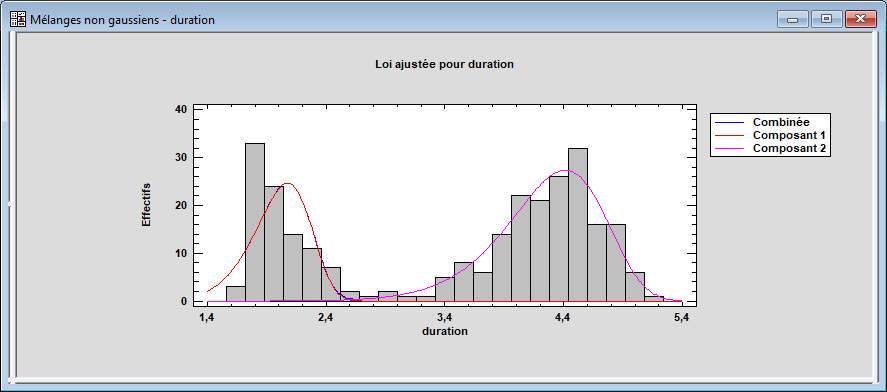
Ajustement de mélanges de lois non gaussiennes

La procédure Ajustement de lois (modèles de mélanges non gaussiens) ajuste une loi à des données numériques continues constituées d’un mélange de deux lois ou plus normales univariées, de Weibull, gamma ou log-normales. Les composants du mélange peuvent représenter différents groupes dans l’échantillon utilisé pour ajuster la loi globale ou un modèle de mélange peut approximer une loi ayant une forme plus complexe.