La méthode de Régression sur Composantes Principales (RCP) est une technique de régression utile lorsque de fortes colinéarités entre les variables explicatives sont présentes et que l’on ne désire pas utiliser les algorithmes de régression pas à pas pour éliminer les variables corrélées entre elles ou les régressions Ridge ou PLS.
Cette technique utilise à la fois l’Analyse en Composantes Principales (ACP) et la Régression Multiple pour élaborer un modèle dont les coefficients sont stables.
Après l’affichage du tableau et de l’histogramme des inerties, vous pouvez choisir le nombre d’axes factoriels à extraire.
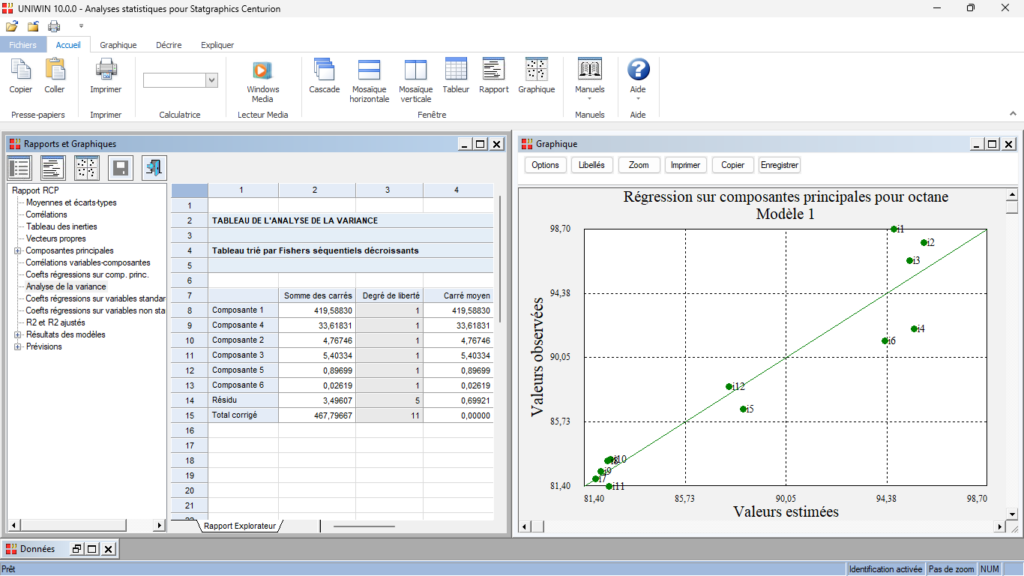
Un rapport général de synthèse est proposé contenant notamment les résultats de l’Analyse en Composantes Principales (ACP), les descriptions des différents modèles de régression et le tableau de l’analyse de la variance.
Les graphiques des cercles factoriels, des plans factoriels, des régressions, des composants et des résidus sont également disponibles.